[ML] 머신러닝 모델(퍼셉트론, 로지스틱 회귀, 서포트 벡터 머신)

- 퍼셉트론(Perceptron)

• 여러 개의 입력을 받아 각각의 값에 가중치를 곱한 후, 모두 더한 것이 출력되는 모델
• 신경망이나 딥러닝의 뿌리가 되는 모델
• 선형 분리 불가능 문제에는 수렴하지 못함

 

 

- 로지스틱 회귀 : 분류를 확률로 생각하는 방식

• 퍼셉트론의 간단함은 유지된 채, 선형 분리 불가능한 문제에서도 적용 가능
• 어느 클래스에 분류 되는 지 구하는것
• 이를 구하기 위해 함수가 필요 → 로지스틱 시그모이드 함수(S자 모양)

e : 네이피어 수라고 불리는 상수

z : 가중치와 데이터 변수의 선형 조합으로 이뤄진 최종 입력

• 시그모이드 함수 모양을 파이썬으로 구현

import matplotlib.pyplot as plt
import numpy as np

# 시그모이드 함수 정의

def sigmoid(z) :
    return 1.0 / (1.0 + np.exp(-z)) # exp : numpy의 지수함수

z = np.arange(-7, 7, 0.1) # 배열 생성
f_x = sigmoid(z)


# 시각화

plt.plot(z, f_x)
plt.axvline(0.0, color = 'k')
plt.ylim(-0.1, 1, 1)
plt.xlabel('z')
plt.ylabel('f(x)')

plt.yticks([0.0, 0.5, 1.0])
ax = plt.gca()
ax.yaxis.grid(True)
plt.tight_layout()
plt.show()

z가 무한으로 커지면 시그모이드 함수는 1에 수렴하게 됨, 반대로 z의 값이 무한으로 작아지면 시그모이드 함수는 0에 수렴하게 됨

• 모든 입력값에 대해 0과 1 사이의 값을 반환한다는 것을 알 수 있음 → 마치 확률처럼!

 

 

- 로지스틱 회귀를 이용하여 선형 분리 가능 문제 생각해보기

• 미지의 데이터 x가 가로로 긴 모양일 때(1)의 확률을 f(x)로 정의 → P(y = 1 | x) = f(x)
• 만약 f(x)의 값이 0.7이라면? 미지의 데이터 x가 가로로 길 확률이 70% → 가로로 긴 것이라 분류됨
• 만약 f(x)의 값이 0.2이라면? 미지의 데이터 x가 세로로 길 확률이 80% → 세로로 긴 것이라 분류됨

 

 

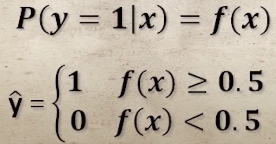
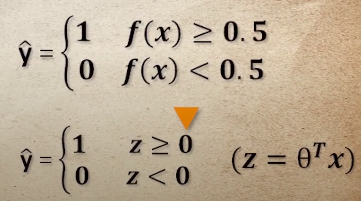
- 결정경계 : 두 가지 중 하나로 구분될 때 유용하게 사용

 

 

- 시그모이드 함수의 매개변수(w) 구하기

1. 목적함수 정의
2. 미분
3. 매개변수 갱신식 구하기

 

 

- 서포트 벡터 머신(Support Vector Machine; SVM)

• 마진을 최대화하기 위한 것
• 레이블을 구분하기 위한 초평면(결정경계)을 그리고 마진을 구함
• 마진 : 초평면과 가장 가까운 훈련 데이터들 사이의 거리

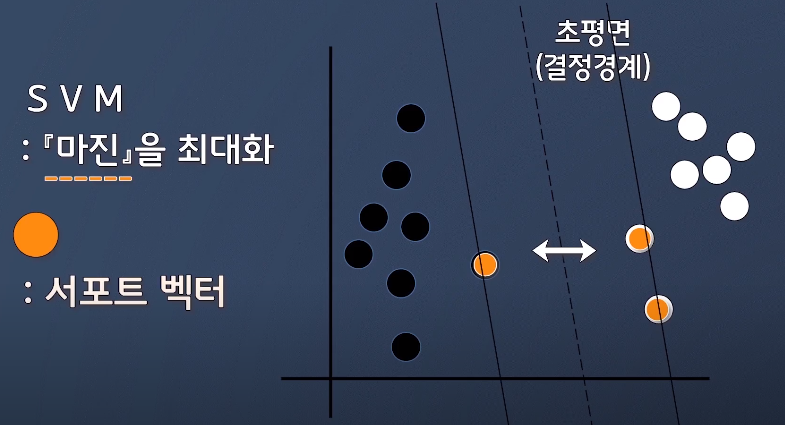
• 선형 분리 불가능 문제에서도 강력한 힘을 발휘
  • 2차원에서만 존재했던 데이터를 3차원 공간으로 옮겨서 SVM은 데이터를 분류하기 위한 분리 가능 공간을 생성, 그리고 다시 2차원 공간으로 옮겨오면 비선형 결정 경계로 바뀌게 됨
• 단점 : 계산비용
  • 2차원 → 3차원으로 매핑하며 새로운 특성 생성 →상당한 컴퓨팅 비용 필요
  • 이러한 높은 비용을 조금이나마 절감하고자 '커널 기법' 등장