[ML] 경사하강법- 미분

- 머신러닝을 적용하는 방법 : 쉽게 말해 함수를 만드는 것

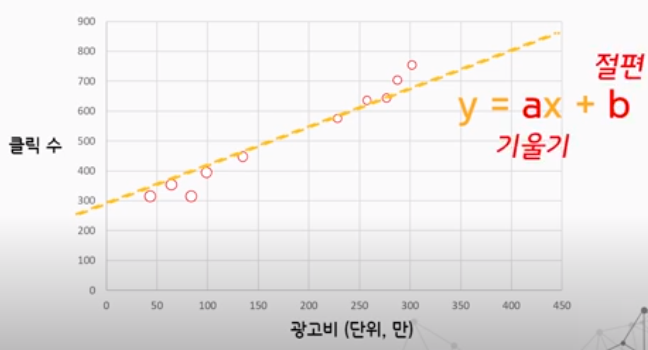
• 그래프의 각각의 점을 지나는 함수의 모양을 알게 되면 광고비를 통해 페이지 노출 횟수를 알 수 있음
• 하지만 노출 횟수에는 노이즈(Noisy Data)가 껴있기 때문에 항상 모든 점을 정확히 지나지는 않음
• 1차함수의 기울기와 절편을 찾는 것이 목표

 

- 머신러닝의 핵심 : 과거의 관측을 기반으로 새로운 샘플의 결과값을 예측

 

- 우리가 바라는 이상 : 적합한 파라미터(parameter), 즉 적합한 가중치와 절편 탐색 → 실제 결과값과 예측 결과값의 차이를 찾아 0을 만드는 것

 

- 우리의 목표 : 어느 정도 현실성을 반영하여, 모든 점에서 생기는 오차의 합계가 가능한 작아지는 함수를 찾는 것 → 오차의 합계식을 목적함수라고 함

제곱을 하는 이유 : 음수가 나올 수도 있기 때문 / 1/2 : 결과로 나온 식을 간단한 모양으로 만들기 위한 상수, 상수로 인해 그래프의 모양이 넓어지거나 좁아질 뿐 최소값의 위치는 변하지 않음

• 목적함수값이 가장 작아지는 파라미터들을 찾는 것이 목표! → 최적화 문제

 

- 경사하강법 : 목적함수의 값을 최소화시키기 위해 마치 경사를 내려가듯 최솟값을 찾는 기법

• 미분 : 어떤 구간에서의 그래프의 기울기를 구하는 것, 간격을 점점 좁혀가며 기울기를 구하는 작업
  • 순간의 변화량을 구하기 위한 함수 f(x), 매우 작은 수 h

함수 f(x)에 있는 점 x에서의 기울기, d/dx : 미분 연산자

또 다른 표현 프라임

6이라는 값이 기울기 = 속도

• 미분의 성질

• 함수의 최솟값
  • g(x) = (x-1)^2
  • 최솟값은 x = 1일 때, g(x) = 0
  • g(x)를 미분하면 d/dx * g(x) = 2x-2 → 미분 후에 나온 함수를 도함수라고 함
  • 도함수가 음수이면 (x<1) g(x) 그래프는 오른쪽 아래로 내려가고
  • 도함수가 0이면 (x=1) g(x) 그래프는 최솟값을 가지며
  • 도함수가 양수이면 (x>1) g(x) 그래프는 오른쪽 위로 올라감(왼쪽 아래로 내려감)
  • 도함수의 부호에 따라 x를 밀어 옮기는 방향이 달라지게 됨
  • 도함수의 부호 반대 방향으로 밀어 옮기게 되면 자연스럽게 최솟값을 향해 움직임
  • 학습률에 따라 최솟값에 도달하기까지 갱신해야 하는 횟수가 달라짐, 수렴되는 속도가 달라짐
  • 학습률의 값을 너무 크게 잡으면 오히려 최솟값에서 멀어지는 '발산'이 일어나고
  • 학습률의 값을 너무 작게 잡으면 최솟값에 수렴하기까지 '많은 시간'이 걸리게 됨 (수렴 속도 지연)

A := B : A를 B에 따라 정의한다.

에타, 양의 정수