728x90
- 정답이 없는 문제를 해결하기 위한 알고리즘 → 비지도학습 '군집분석'
- 군집분석(Clustering Analysis)
- ex) 쇼핑몰에서 페이지 체류 시간, 구매 금액대 등을 토대로 소비자 유형 그룹을 나누고(군집 설정), 새로운 소비자가 쇼핑몰에 들어왔을 때 행동을 바탕으로 앞서 설정해놓은 그룹으로 할당, 비슷한 소비자가 구매한 상품 노출하여 제품 구매율을 높힘
- 군집은 정답을 모르는 데이터 안에서 숨겨진 구조를 찾는 것
- 클래스 레이블이 없는 데이터를 특정 군집으로 묶고자 할 때 활용
- 계층 군집, 밀집도 기반 군집(클러스터 모양이 원형이 아닐 때 사용)
- K-평균(K-means)
- 매우 쉬운 구현성, 높은 계산 효율성 → 학계와 산업현장을 가리지 않고 활약
- 프로토타입 기반 군집 : 각 클러스터가 하나의 프로토타입으로 표현됨
- 프로토타입(Prototype)
- 연속적인 특성에서는 비슷한 데이터 포인트의 센트로이드(centroid - 평균)
- 범주형 특성에서는 메도이드(medoid - 가장 자주 등장하는 포인트)
- 프로토타입(Prototype)
- 원형 클러스터 구분에 뛰어남
- 사전에 몇 개의 클러스터를 만들 것인지 직접 지정해줘야함 → 주관적인 사람의 판단 개입
- 적절한 K값을 선택했다면 높은 성능, 부적합한 K값은 모델의 성능을 보장할 수 없음
- 파이썬 활용하여 K-평균 군집분석 진행하기
# 무작위 데이터셋 생성
from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples = 150, # 150개
n_features = 2, # 2차원
centers = 3, # 3개의 클러스터 혹은 중심
cluster_std = 0.5, # 클러스터의 표준편차 값
shuffle = True, # 무작위로 섞을 지 여부
random_state = 0) # 시드 값
#시각화 : 2차원 산점도 그리기
import matplotlib.pyplot as plt
plt.scatter(X[:, 0], X[:, 1], c = 'white', marker = 'o', edgecolor = 'black', s= 50)
plt.grid()
plt.tight_layout()
plt.show()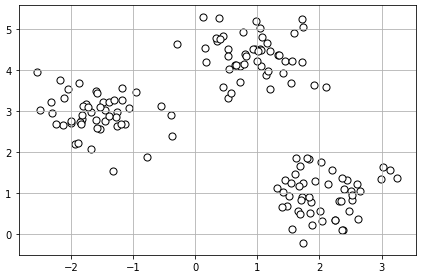
- 목표 : 특성의 유사도에 기초하여 데이터들을 그룹으로 모으는 것
- K-평균 4단계 알고리즘
- 데이터 포인트에서 랜덤하게 K개의 센트로이드를 초기 클러스터 중심으로 선택
- 각 데이터를 가장 가까운 센트로이드에 할당
- 할당된 샘플들을 중심으로 센트로이드를 이동
- 클러스터 할당이 변하지 않거나, 사용자가 지정한 허용오차나 최대 반복횟수에 도달할 때 까지 2/3 과정 반복
- 유사도 측정 방법
- 임의의 차원 공간에 있는 두 데이터 포인트 x와 y사이의 유클리디안 거리 혹은 유클리디안 거리 제곱 지표 기반 → 최적화 문제
- 클러스터 내의 제곱 오차합(SSE)을 반복적으로 최소화
- 각 데이터를 센트로이드에 할당할 때마다, 센트로이드는 이동 → 센트로이드가 변화할 때마다 오차 제곱합을 반복적으로 계산하면서 변화량에 대한 허용 오차값이 일정 수준내로 들어온다면 더 이상 클러스터가 변화하지 않는다는 것이고, 최적화가 완료되었다는 것

- 각 점들간의 거리를 측정할 때, 점들간의 단위와 변동폭이 크다면 왜곡 발생 → 거리 산출 시 불필요한 항목간의 특성을 제거하고 단위를 일치시키는 '표준화'과정으로 왜곡을 줄일 수 있음
from sklearn.cluster import KMeans
km = KMeans(n_clusters = 3, # 클러스터 개수 3개
init = 'random', # K평균 알고리즘 설정, 초기 중심 좌표를 무작위로 선정하여 random
n_init = 10, # 각기 다른 랜덤한 센트로이드에서 독립적으로 몇 번 실행하여 가장 낮은 제곱오차합을 만들 것인지 설정
max_iter = 300, # 최대 몇 번을 반복할 것인지
tol = 1e-04, # 허용 오차값
random_state = 0)
# 군집분석 알고리즘에 의한 예측 클래스 레이블
y_km = km.fit_predict(X)
# 시각화
import matplotlib.pyplot as plt
plt.scatter(X[y_km == 0, 0], X[y_km == 0, 1],
s = 50, c = 'lightgreen', marker = 's', edgecolor = 'black', label = 'cluster 1')
plt.scatter(X[y_km == 1, 0], X[y_km == 1, 1],
s = 50, c = 'orange', marker = 'o', edgecolor = 'black', label = 'cluster 2')
plt.scatter(X[y_km == 2, 0], X[y_km == 2, 1],
s = 50, c = 'lightblue', marker = 'v', edgecolor = 'black', label = 'cluster 3')
plt.scatter(km.cluster_centers_[:, 0], km.cluster_centers_[:,1],
s = 250, marker = '*', c = 'red', edgecolor = 'black', label = 'centroids')
plt.legend(scatterpoints = 1)
plt.grid()
plt.tight_layout()
plt.show()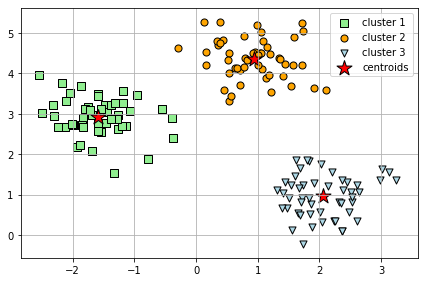
- 초기 센트로이드를 설정할 때, 랜덤으로 위치를 선정하기 때문에 애초에 잘못 선정된 곳에서 시작한 경우 (여기에 더불어 데이터가 적은 악조건이 붙게 된다면) 클러스터의 성능이 매우 불안정해짐
- 따라서 초기 클러스터 센트로이드를 좀 더 똑똑하게 할당할 수 있는 기법 등장 → K-means++
- K-means 알고리즘에서 클러스터는 중첩되지 않고 계층적이지 않음, 클러스터 당 하나 이상의 데이터가 존재 → 데이터가 꼭 하나의 클러스터로만 구분되지 않을 경우 문제 발생 → K-means++
- K-means++
km = KMeans(n_clusters = 3, # 클러스터 개수 3개
init = 'k-means++', # K평균++ 알고리즘 설정
n_init = 10, # 각기 다른 랜덤한 센트로이드에서 독립적으로 몇 번 실행하여 가장 낮은 제곱오차합을 만들 것인지 설정
max_iter = 300, # 최대 몇 번을 반복할 것인지
tol = 1e-04, # 허용 오차값
random_state = 0)
y_km = km.fit_predict(X)- K-평균의 무작위성을 보완하기 위한 기법
- 초기 센트로이드가 서로 멀리 떨어지도록 위치 시킴
- 기본 K-평균보다 일관되고 좋은 결과 보여줌
- 사이킷런 사용하여 군집의 품질 평가하기
- 비지도학습은 올바른 정답이 없기 때문에 군집의 품질을 평가해야 하는 경우 알고리즘 자체의 지표를 사용해야함 ex) k-평균 군집의 성능 비교를 위한 오차 제곱합
- KMeans 모델 학습을 진행한 객체 안에 관성이라는 뜻을 가진 'inertia' 속성안에 이미 계산이 완료 되어 있음
print('왜곡 : %.2f' % km.inertia_)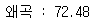
- 왜곡 값이 적절한 값인지는 k를 다양한 값으로 할당한 후에 왜곡값을 비교해봐야함 → 엘보우 방법
- 엘보우 방법(elbow method)
- 최적인 클러스터 개수 k를 추정
- k값의 증가 → 센트로이드의 증가 →데이터들이 센트로이드에 더 가까워지는 것 → 왜곡값(SSE)의 감소
# k를 1부터 10까지 구축, 각각의 SSE를 시각화
distortions = []
for i in range(1, 11) :
km = KMeans(n_clusters = i,
init = 'k-means++',
n_init = 10,
max_iter = 300,
random_state = 0)
km.fit(X)
distortions.append(km.inertia_)
plt.plot(range(1,11), distortions, marker = 'o')
plt.xlabel('Number of clusters')
plt.ylabel('Distortion')
plt.tight_layout()
plt.show()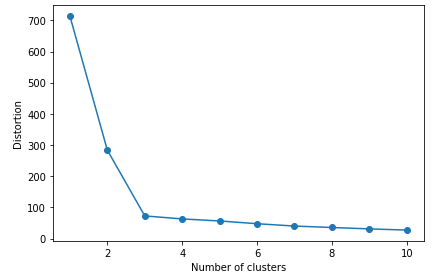
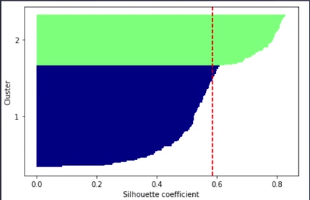
- 실루엣 분석(silhouette analysis)
- 군집 품질을 평가하는 또 다른 방법
- 클러스터 내 데이터들이 얼마나 조밀하게 모여있는지를 측정하는 그래프 도구

- 계수 구하는 방법
- 하나의 임의의 데이터(x(i))와 동일한 클러스터 내의 모든 다른 데이터 포인트 사이의 거리를 평균하여 클러스터의 응집력(a(i))을 계산
- 앞서 선정한 데이터와 가장 가까운 클러스터의 모든 샘플간 평균 거리로 최근접 클러스터의 클러스터 분리도(b(i))를 계산
- 클러스터 응집력과 분리도 사이의 차이를 둘 중 큰 값으로 나눠 실루엣 계수(s(i))를 계산
- 분리도 = 응집력 : 실루엣 계수는 0이 됨, 클러스터가 중첩되어 있다는 의미
- 분리도 > 응집력 : 이상적인 실루엣 계수인 1에 가깝게 됨
- 분리도 : 데이터가 다른 클러스터와 얼마나 다른지를 나타냄
- 응집력 : 클러스터 내 다른 샘플과 얼마나 비슷한지를 나타냄, 작을수록 클러스터 내 다른 데이터들과 비슷함
import numpy as np
from matplotlib import cm
from sklearn.metrics import silhouette_samples
# sklearn의 metrics 모델 안에 silhouette_samples함수로 계산
# k-means++ 알고리즘
km = KMeans(n_clusters = 3,
init = 'k-means++',
n_init = 10,
max_iter = 300,
tol = 1e-04,
random_state = 0)
y_km = km.fit_predict(X)
cluster_labels = np.unique(y_km)
n_clusters = cluster_labels.shape[0]
# 실루엣 분석
silhouette_vals = silhouette_samples(X, y_km, metric = 'euclidean')
# 시각화
y_ax_lower, y_ax_upper = 0, 0
yticks = []
for i, c in enumerate(cluster_labels) :
c_silhouette_vals = silhouette_vals[y_km == c]
c_silhouette_vals.sort()
y_ax_upper += len(c_silhouette_vals)
color = cm.jet(float(i) / n_clusters)
plt.barh(range(y_ax_lower, y_ax_upper), c_silhouette_vals, height = 1.0,
edgecolor = 'none', color = color)
yticks.append((y_ax_lower + y_ax_upper) / 2)
y_ax_lower += len(c_silhouette_vals)
silhouette_avg = np.mean(silhouette_vals)
plt.yticks(yticks, cluster_labels + 1)
plt.ylabel('Cluster')
plt.xlabel('Silhouette coefficient')
plt.tight_layout()
plt.show()
728x90
'AI > Machine Learning' 카테고리의 다른 글
| [ML] 강화학습 (0) | 2021.05.13 |
|---|---|
| [ML] 군집분석(계층 군집, 밀집도 기반 군집) (0) | 2021.05.12 |
| [ML] 머신러닝 모델(결정 트리 학습, K-근접 이웃) (0) | 2021.05.11 |
| [ML] 머신러닝 모델(퍼셉트론, 로지스틱 회귀, 서포트 벡터 머신) (0) | 2021.05.11 |
| [ML] 경사하강법 - 편미분 (0) | 2021.05.10 |




댓글