[DL] 퍼셉트론(perceptron)

- '맥컬록-피트 뉴런(MCP)'

• 1943년 워랜 맥컬록 & 윌터 피츠 : AI를 설계하기 위해, 생물학적 뇌가 동작하는 방식을 이해하려는 시도 → 간소화된 뇌의 뉴런 개념 발표
• 신경세포를 이진 출력을 내는 간단한 논리 회로로 표현

 

 

- Perceptron

• 1957년 프랭크 로젠 블렛 : MCP 뉴런 모델을 기반으로 퍼셉트론 학습 개념을 처음 발표
• 자동으로 최적의 가중치를 학습하는 알고리즘 제안
• 가중치는 뉴런의 출력 신호를 낼지 말지를 결정하기 위해 입력 특성에 곱하는 계수
• 입력을 받아 계산한 후 출력을 반환하는 구조

뉴런이 여러 개 모여 레이어 구성, 레이어가 다시 모여 구성된 형태

뉴런의 구조, 가중치와 활성화 함수가 숨어 있음

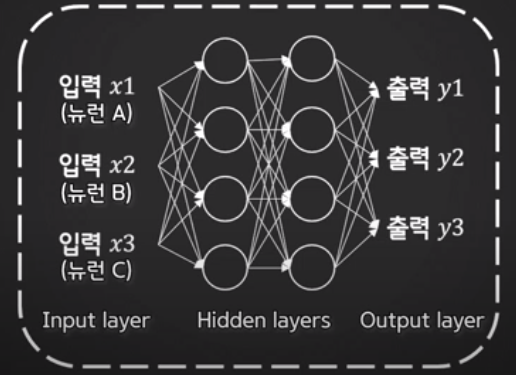
• 활성화함수 : 뉴런의 출력 값을 정하는 함수
• 뉴런에서 학습할 때 변하는 것은 가중치
  • 가중치는 처음에 초기화를 통해 무작위 값을 넣고 학습과정에서 일정한 값으로 수렴
  • 학습이 잘 된다는 것은 좋은 가중치를 얻어 원하는 출력에 점점 가까워지는 값을 얻는 것

 

 

- '헵의 학습 규칙'

• 1949년 Donald O. hebb : 인간 두뇌의 작용은 개별 신경세포에 의해서 이뤄지는 것이 아닌, 그들간의 연결 강도로 정해진다는 '연결주의' → 우리의 두뇌가 신경망으로 활동하고 있음을 설명
• 만약 시냅스가 양쪽 뉴런이 동시에 반복적으로 활성화되었다면 그 뉴런 사이의 연결 강도가 강화된다는 관찰에 근거
• 이후 신경망 모델들의 학습 규칙의 토대가 됨

 

 

- 퍼셉트론 파이썬 코드로 확인해보기

import tensorflow as tf

tf.compat.v1.set_random_seed(2020)

# 입력값
x = 1

# 출력값
y = 0

# 가중치 : 정규분포의 무작위 값
w = tf.random.normal([1], 0, 1)

# 활성화 함수 : 시그모이드
import math

def sigmoid(x) :
    return 1/(1 + math.exp(-x))

output = sigmoid(x * w)
print(output)

• 출력값이 0과는 차이가 있음 → 가중치를 무작위 선정하였기 때문(가중치가 적합하지 않았다)
• error = 기대출력 - 실제출력

for i in range(1000) :
    output = sigmoid(x*w)
    error = y - output
    
    # 가중치 조절(갱신) : 경사하강법
    # w = w + x * n(학습률) * error
    # 학습률 : 가중치 조정을 위한 하이퍼파라미터
    w = w + x * 0.1 * error 
    
    if i%100 == 99 :
        print('학습 횟수 : ', i, 'Error : ', error, '예측 결과 : ', output)

x =0
y = 1
w = tf.random.normal([1], 0, 1)

for i in range(1000) :
    output = sigmoid(x*w)
    error = y - output
    w = w + x * 0.1 * error 
    
    if i%100 == 99 :
        print('학습 횟수 : ', i, 'Error : ', error, '예측 결과 : ', output)

• 위의 경우, 우리가 원하는 출력값을 얻을 수 없음
• 왜? 입력값이 0이기 때문에 어떠한 학습률값을 넣어도 가중치 조정이 의미가 없음
• 이러한 경우를 방지하고자 '편향' 개념 등장
• 편향 : 한쪽으로 치우쳐진 고정 값, 입력값이 0인 경우에 아무것도 학습하지 못하는 것 방지
• 편향값도 가중치처럼 난수로 초기화되며 뉴런에 더해져 출력을 계산

  x =0
  y = 1
  w = tf.random.normal([1], 0, 1)
  b = tf.random.normal([1], 0, 1) # 편향 추가
  
  for i in range(1000) :
      output = sigmoid(x * w + 1 * b)
      error = y - output
      w = w + x * 0.1 * error 
      b = b + 1 * 0.1 * error
      
      if i%100 == 99 :
          print('학습 횟수 : ', i, 'Error : ', error, '예측 결과 : ', output)​

우리가 원하는 값에 수렴하는 값 출력

 

 

- AND 연산 : 입력값이 모두 참인 경우에만 참을 출력, 나머지 경우는 모두 거짓 출력

import numpy as np
import tensorflow as tf

x = np.array([[1,1], [1,0], [0,1], [0,0]])
y = np.array([[1], [0], [0], [0]])
w = tf.random.normal([2], 0, 1)
b = tf.random.normal([1], 0, 1)
b_x = 1

for i in range(2000) :
    error_sum = 0
    for j in range(4) :
        output = sigmoid(np.sum(x[j]*w)+b_x*b)
        error = y[j][0] - output
        w = w + x[j] * 0.1 * error 
        b = b + b_x * 0.1 * error
        error_sum += error
        
for i in range(4) :
    print('X : ', x[i], 'Y :', y[i], 'Output : ', sigmoid(np.sum(x[i]*w)+b))

 

 

- OR연산 : 모든 입력값이 거짓일 때만 거짓을 출력, 나머지 경우는 모두 참 출력

import numpy as np
import tensorflow as tf

x = np.array([[1,1], [1,0], [0,1], [0,0]])
y = np.array([[0], [0], [0], [1]])
w = tf.random.normal([2], 0, 1)
b = tf.random.normal([1], 0, 1)
b_x = 1

for i in range(2000) :
    error_sum = 0
    for j in range(4) :
        output = sigmoid(np.sum(x[j]*w)+b_x*b)
        error = y[j][0] - output
        w = w + x[j] * 0.1 * error 
        b = b + b_x * 0.1 * error
        error_sum += error
        
for i in range(4) :
    print('X : ', x[i], 'Y :', y[i], 'Output : ', sigmoid(np.sum(x[i]*w)+b))

 

 

- XOR 연산 : 2개의 입력값이 서로 다를 때 참을 출력

import numpy as np
import tensorflow as tf

x = np.array([[1,1], [1,0], [0,1], [0,0]])
y = np.array([[0], [1], [1], [0]])
w = tf.random.normal([2], 0, 1)
b = tf.random.normal([1], 0, 1)
b_x = 1

for i in range(2000) :
    error_sum = 0
    for j in range(4) :
        output = sigmoid(np.sum(x[j]*w)+b_x*b)
        error = y[j][0] - output
        w = w + x[j] * 0.1 * error 
        b = b + b_x * 0.1 * error
        error_sum += error
        
for i in range(4) :
    print('X : ', x[i], 'Y :', y[i], 'Output : ', sigmoid(np.sum(x[i]*w)+b))

• 모든 결과값이 0.5 근처에 머물며 우리가 원하는 값으로 수렴하지 않음

단층이 아닌 다층 퍼셉트론을 활용하면 해결할 수 있음

• 1969년 당시 연구진 : 퍼셉트론은 간단한 XOR문제 조차 풀 수 없는 단순선형분류기 → 퍼셉트론의 한계, 인공신경망 연구의 겨울
• 198년 다수의 연구진이 다층 퍼셉트론 제시 : 은닉층을 활용하여 선형 분류 판별선을 여러 개 그리는 효과를 얻음으로써 XOR 문제를 해결 가능
• 하지만 다층 퍼셉트론의 파라미터 개수가 많아지면서 적절한 가중치와 편향을 학습하는데 어렵다는 약점
• 이를 해결하기 위해 1986년 제프리 힐튼 '역전파 알고리즘'
• 이를 통해 다층 퍼셉트론은 인공지능 연구를 가속화시켜주는 계기가 됨